Strength
First, there is more than one kind of strength. A polymer sample has tensile strength if it is strong when one pulls on it. Tensile strength is important for a material that is going to be stretched or under tension. Fibers need good tensile strength. A polymer sample has compressional strength if it is strong when one tries to compress it. Concrete is an example of a material with good compressional strength. Anything that has to support weight from underneath has to have good compressional strength. A polymer sample has flexural strength if it is strong when one tries to bend it. Additionally, a polymer sample has torsional strength if it is strong when one tries to twist it, and has impact strength if it is strong when one hits it sharply and suddenly, as with a hammer.
To measure the tensile strength of a polymer sample, we usually stretch it with a machine such as an Instron. This machine simply clamps each end of the sample, then, when you turn it on it stretches the sample. While it is stretching the sample, it measures the amount of force (F) that it is exerting. When we know the force being exerted on the sample, we then divide that number by the cross-sectional area (A) of our sample. The answer is the stress that our sample is experiencing.
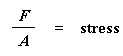
Then, using the machine, we continue to increase the amount of force and stress naturally on the sample until it breaks. The stress needed to break the sample is the tensile strength of the material.
Likewise, one can imagine similar tests for compressional or flexural strength. In all cases, the strength is the stress needed to break the sample.
Since tensile stress is the force placed on the sample divided by the cross-sectional area of the sample, tensile stress and tensile strength are both measured in units of force divided by units of area, usually N/cm2. Stress and strength can also be measured in megapascals (MPa) or gigapascals (GPa). It's easy to convert between the different units, because 1 MPa = 100 N/cm2, 1 GPa = 100,000 N/cm2, and of course 1 GPa = 1,000 MPa.
Other times, stress and strength are measured in the old English units of pounds per square inch, or psi. If you ever have to convert psi to N/cm2, the conversion factor is 1 N/cm2 = 1.45 psi.
Elongation
Elongation is a type of deformation. Deformation is simply a change in shape that anything undergoes under stress. Usually we talk about percent elongation, which is just the length the polymer sample is after it is stretched (L), divided by the original length of the sample (L0), and then multiplied by 100.
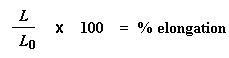
There are a number of things we measure related to elongation. Which is most important depends on the type of material one is studying. Two important things we measure are ultimate elongation and elastic elongation.
Ultimate elongation is important for any kind of material. It is nothing more than the amount you can stretch the sample before it breaks. Elastic elongation is the percent elongation you can reach without permanently deforming your sample. That is, how much can you stretch it, and still have the sample snap back to its original length once you release the stress on it. This is important if your material is an elastomer. Elastomers have to be able to stretch a long distance and still bounce back. Most of them can stretch from 500 to 1000 % elongation and return to their original lengths without any trouble.
Modulus
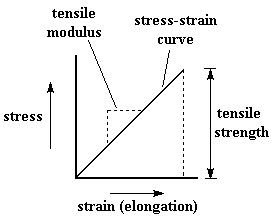
Elastomers need to show high elastic elongation. But for some other types of materials, like plastics, it is usually better that they do not stretch or deform so easily. To know how well a material resists deformation, modulus is measured. To measure tensile modulus, we do the same thing as we did to measure strength and ultimate elongation. This time we measure the stress we're exerting on the material, just like we did when we were measuring tensile strength. We slowly increase the amount of stress, and then measure the elongation the sample undergoes at each stress level. We keep doing this until the sample breaks. Then we make a plot of stress versus elongation, like this:
There are times when the stress-strain curve isn't nice and straight, like we saw above. For some polymers, especially flexible plastics, we get odd curves that look like this:
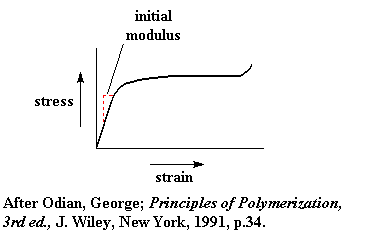
The slope isn't constant as stress increases. The slope, that is the modulus, is changing with stress. In a case like this we usually regard the initial slope as the modulus, as you can see in the stress-strain curve above.
In general, fibers have the highest tensile modulus, elastomers have the lowest, and plastics have tensile modulus between fibers and elastomers.
Modulus is measured by calculating stress and dividing by elongation, and would be measured in units of stress divided by units of elongation. But since elongation is dimensionless, it has no units by which we can divide. So modulus is expressed in the same units as strength, such as N/cm2.
Toughness
The plot of stress versus strain mentioned above can give us another very valuable piece of information. If one measures the area underneath the stress-strain curve, colored red in the graph below, the number we get is called toughness.
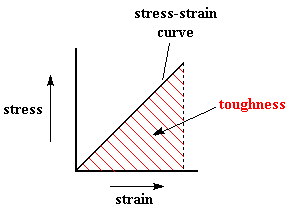
Toughness is a measure of the energy a sample can absorb before it breaks. If the height of the triangle in the plot is strength, and the base of the triangle is strain, then the area is proportional to strength times strain. Since strength is proportional to the force needed to break the sample, and strain is measured in units of distance (the distance the sample is stretched), then strength times strain is proportional is force times distance, and as we remember from physics, force times distance is energy.
How is toughness different from strength? From a physics point of view, the answer is that strength tells how much force is needed to break a sample, and toughness tells how much energy is needed to break a sample. But that doesn't really tell you what the practical differences are.
What is important is knowing that just because a material is strong, it isn't necessarily going to be tough as well. We'll look at the graph below to show this.
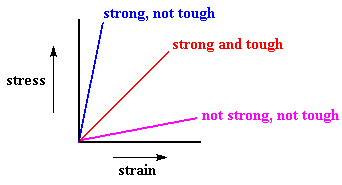
The blue plot is the stress-strain curve for a sample that is strong, but not tough. As you can see, it takes a lot of force to break this sample, but not much energy, as there isn't much area underneath the curve. Likewise, this sample can't stretch very far before it breaks. A material like this which is strong, but can't deform very much before it breaks is called brittle.
The red plot is a stress-strain curve for a sample that is both strong and tough. This material is not as strong as the sample in the blue plot, but the area underneath its curve is a lot larger than the area under the blue sample's curve. So it can absorb a lot more energy than the blue sample can, for the red sample elongates a lot more before breaking than the blue sample does. Deformation allows a sample to dissipate energy. If a sample can't deform, the energy won't be dissipated, and will cause the sample to break.
Mechanical Properties of Real Polymers
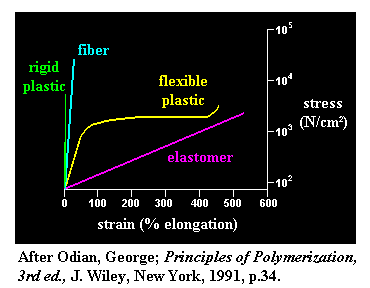
The big graph above compares typical stress-strain curves for different kinds of polymers. In the green plot, a rigid plastics such as polystyrene, poly(methyl methacrylate or polycarbonate can withstand a good deal of stress, but they won't withstand much elongation before breaking. There isn't much area under the stress-strain curve at all. So materials like this are strong, but not very tough. And the slope of the plot is very steep, which means that it takes a lot of force to deform a rigid plastic. So it's easy to see that rigid plastics have high modulus. In short, rigid plastics tend to be strong, resist deformation, but they tend not to be very tough, that is, they're brittle.
Flexible plastics like polyethylene and polypropylene are different from rigid plastics in that they don't resist deformation as well, but they tend not to break. The ability to deform is what keeps them from breaking. Initial modulus is high, namely, it will resist deformation for awhile, but if enough stress is put on a flexible plastic, it will eventually deform. The bottom line is that flexible plastics may not be as strong as rigid ones, but they are a lot tougher.
It is possible to alter the stress-strain behavior of a plastic with additives called plasticizers. A plasticizer is a small molecule that makes plastics more flexible. For example, without plasticizers, poly(vinyl chloride), or PVC for short, is a rigid plastic. Rigid unplasticized PVC is used for water pipes. But with plasticizers, PVC can be made flexible enough to use to make things like inflatable swimming pool toys.
Fibers like KevlarTM , carbon fiber and nylon tend to have stress-strain curves like the aqua-colored plot in the graph above. Like the rigid plastics, they are more strong than tough, and don't deform very much under tensile stress. But when strength is what you need, fibers have plenty of it. They are much stronger than plastics, even the rigid ones, and some polymeric fibers, like KevlarTM, carbon fiber and ultra-high molecular weight polyethylene have better tensile strength than steel.
Elastomers like polyisoprene, polybutadiene and polyisobutylene have completely different mechanical behavior from the other types of materials. In the pink plot, elastomers have very low modulus that can tell from the very gentle slope of the pink plot.
But it takes more than just low modulus to make a polymer an elastomer. Being easily stretched is not much use unless the material can bounce back to its original size and shape once the stress is released. Rubber bands would be useless if they just stretched and didn't bounce back. Elastomers do bounce back, and that's what makes them so amazing. They have not just high elongation, but high reversible elongation.